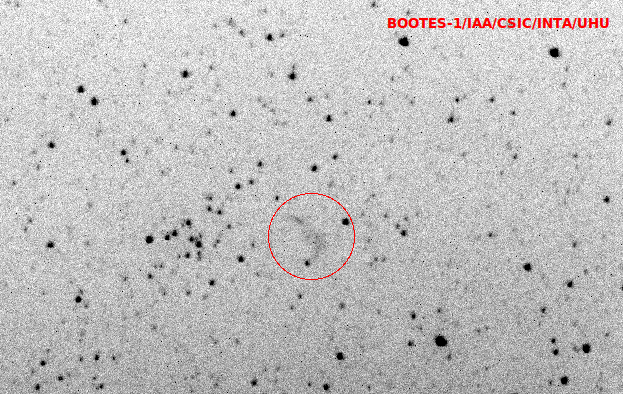
En la madrugada del pasado 21 de enero se produjo un eclipse total de Luna coincidiendo con una súper Luna, es decir, cuando en fase llena nuestro satélite está más cercano (perigeo). En este artículo recopilamos parte del material que se ha recogido con los instrumentos de la Red de Seguimiento de bólidos y meteoros de la SMA y de la Red BOOTES (IAA/CSIC) así como por parte de numerosos socios que lo observaron.
Arriba se representa el gráfico obtenido por el medidor del brillo del fondo del cielo (SQM) de nuestra estación en Dehesa San Francisco (SMA/Fundación Monte Mediterráneo). Si la gráfica baja significa que el cielo se hace más brillante. Cuando sube, se oscurece. Como se trataba de una súper Luna, el brillo es tal que, a partir de la medianoche se sale incluso del cuadro por la parte de abajo. Pero conforme comienza el eclipse, el cielo se hace poco a poco más oscuro hasta que la Luna entra por completo en la sombra de la Tierra. Esta fase de totalidad se reconoce en la especie de meseta en la que permanece con una magnitud cercana a la 22. Al finalizar la totalidad, de nuevo se vuelve el cielo cada vez más brillante hasta que el instrumento dejó de tomar medidas porque llegaba el amanecer.
La cámara de todo el cielo del observatorio BOOTES-2 (IAA/CSIC/UMA) toma imágenes en forma continua cada minuto. Con parte de ellas hemos confeccionado este time/lapses. Adviértase que apenas si se ven estrellas mientras luce la enorme súper Luna, pero cómo aumenta considerablemente su número al llegar la fase de eclipse total. Por desgracia el telescopio del observatorio, a mano izquierda, impide ver la reaparición de la Luna tras la totalidad.
El de abajo es otro time/lapses generado a partir de las imágenes de la cámara de todo el cielo de la estación del Observatorio del Torcal (SMA/OAT).
Nuestros socios Rosa López, plácido Toval, Francisco Gálvez y Blanca Troughton tomaron las siguientes fotografías, bien con ayuda de instrumentación óptica o con un simple teléfono móvil:
Además, Francisco Gálvez (SMA, Aula del Cielo y OAT) y José Manuel Núñez (SMA y OAT) realizaron un completo seguimiento del eclipse con varios telescopios. La siguiente es una de sus composiciones cuyo objeto es el de dar una idea de la sombra de la Tierra por la que pasa la Luna:
En la composición fotográfica de abajo se resalta el borde hipotético de la sombra de la Tierra:
Sobre cuál es el diámetro de la sombra de la Tierra a la distancia de la Luna se puede plantear un interesante problema cuya resolución solo requiere de matemáticas elementales. En efecto, el día 21 de enero a la hora del eclipse la Tierra se hallaba a una distancia de 0,98402276 U.A. (unidades astronómicas) del Sol, y a 0,00237063 U.A. de la Luna. La Unidad Astronómica es una medida de longitud que equivale a 149.597.870,7 Km.
Convirtiendo a quilómetros, el Sol estaba a 147.207.709,6 Km, y la Luna a 354.641,2 Km. Suponiendo que tanto la Tierra como el Sol son esferas perfectas, nuestro planeta proyecta una sombra con forma de cono:
El rayo de Sol que parte del punto Q (véase esquema superior) pasa tangente a la Tierra hasta el vértice C del cono de sombra. Ahora hay que recordar el teorema de Thales y aplicarlo a los triángulos (C,P,T) y (C,Q,S). Según él, el radio de la Tierra PT es al radio del Sol QS como la distancia entre C y T es a la distancia entre C y S. Los radios anteriores son conocidos, en concreto, la Tierra tiene un radio medio de 6.371 Km, y el Sol de 695.408 Km.
Con los datos anteriores se resuelve una sencilla ecuación obteniendo que el vértice de la sombra terrestre se halla a 1.361.117,5 Km. Ahora basta aplicar de nuevo el teorema de Thales a los triángulos (C,L,U) y (C,T,R):
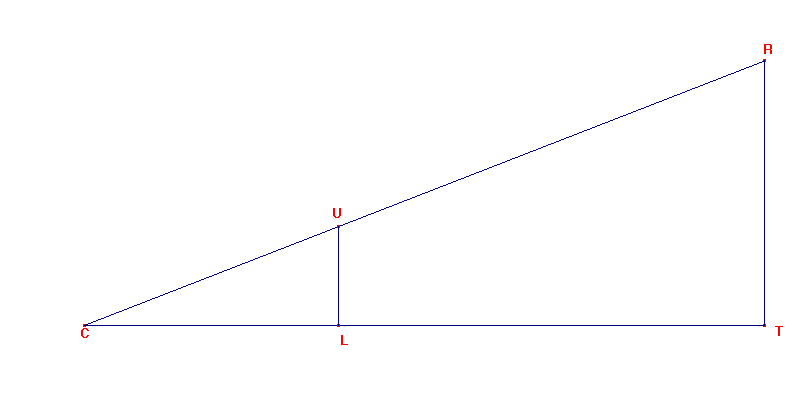donde L es el centro de la Luna, y RT es el radio terrestre. De aquí se obtiene un radio de la sombra terrestre a la distancia lunar (distancia entre U y L) de 4.711 Km, es decir, un diámetro de 9.422 Km.
